普象-让好设计发光

为实现空间拍摄功能，iphone16的摄像头采用竖向跑道圆设计，这样设计也可与前代方块模组做区分。更换新元素能直观表达产品更新换代。

iPhone X等旧机型也曾使用跑道圆设计，iPhone16重新使用这一元素，亦能串联起消费者的品牌记忆。

无论跑道圆还是矩形，这些几何元素容纳了内部模组，也关乎产品外在形象。外部特征决定了产品辨识度，它们的设计至关重要。

例如，其他品牌摄像头常以硕大的尺寸和精致的细节向消费者展示强大的影像能力。

图片源自：小米官网

而跑道圆这一元素基础又常见，Apple多年反复使用，展现出一种不变应万变的态度。当我们谈论Apple的设计时，总是关乎“极简” “功能主义”这样的词汇，Apple坚持这样的设计，也就不足为奇了。

仔细观察iPhone16的跑道圆，它的轮廓曲线符合人们对Apple Design的预期：曲率流畅，线条过渡自然。

这种使用贝塞尔曲线绘制的平滑跑道圆如今已很常见，很多设计中都能看到它。

图片源自：layer官网

图片源自：google官网

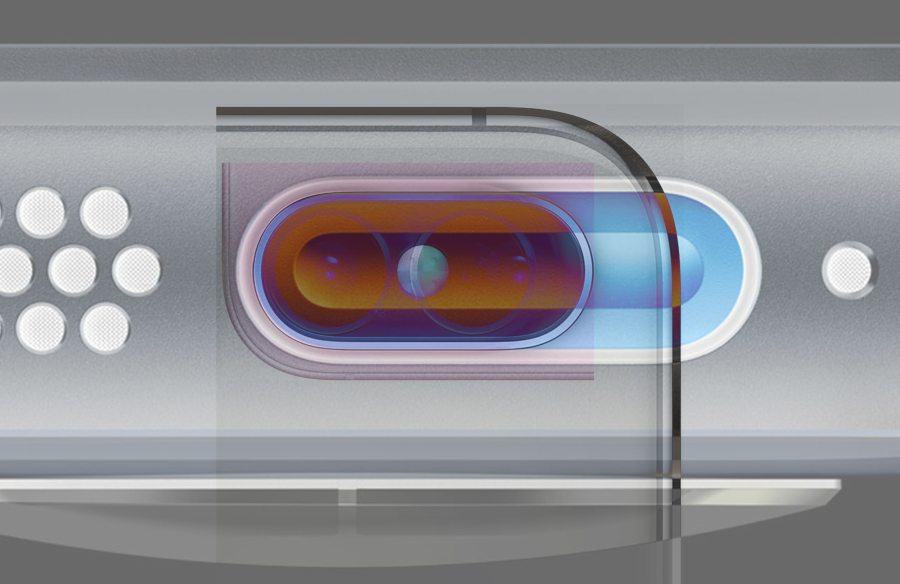
将Apple产品中的跑道圆元素如摄像头，按钮，灵动岛，在Photoshop中叠加，会发现它们的曲线轮廓一致。

公共舆论常批评苹果设计缺乏变化，创新缓慢。人们对新的形式总是有无尽的渴望，这些批评的声音反映了用户欲望与现实之间的落差。

但也可换个角度看：是什么使得苹果坚持使用同样的形态轮廓，仿佛认定这就是最完美的答案？

在西方文化传统里，人们普遍认为真正的美具备必然性、纯洁性和绝对完美的特质。这一观念最早可以追溯到古希腊时期，当时的哲学家柏拉图对此有这样的论述：

“我所说的形式美，……不是……关于动物或植物的美的，而是直线和圆，以及用尺、规和矩形形成的平面形和立体形。这些形状的美不像别的事物是相对的，而是按照他们的本质就永远是绝对美的。……它们的美……不是从对其他事物的关系来的，而是绝对的是从他们的本质来的。”

摘自吴琼《西方美学史》，原文来自朱光潜编纂的《柏拉图文艺对话集》

柏拉图的美学观源自毕达哥拉斯学派。毕达哥拉斯则是最早通过数学研究世界的哲学家，他认为“数”是万物的本源，数的原则统治宇宙中的一切。

毕氏学派和柏拉图的美学观对后世影响极为深远，中世纪的宗教哲学家，甚至揣测上帝也是使用圆规来测量世界，并以此给世界制定规则和尺度。

中世纪书籍插图，图片摘自《美的历史》，[意]翁贝托-艾科

我们再看看（前）Apple工业设计负责人 Jonathan Ive 如何描述自己的美学观：

“I think … forms … are not justarbitrary shapes, it feels almost inevitable, it feels almost un-designed. It feels almost like, well of course it`s that way, why wouldn`t it be any otherway.”

“我认为（产品的）形式不（应该）是那种随心所欲的形状，（而是应该让人）感觉那样是必然的，感觉就像，没有被设计过似的，那种感觉就像是，它本来就是那样，而不应该是别的样子。”

内容来自纪录片《objectified》

Ive的观点，柏拉图一定会点头赞同。

大胆设想一下，Apple的跑道圆，可能也存在某种必然性，其形态应由逻辑推导所得，而非任由模糊不定的“感觉” “直觉”，来提供绝对的判断。

用两条平行直线连接两个半圆，可以得到一个我们熟悉的跑道圆。

这种跑道圆在曲线与直线相接的地方会显得不够平滑，因为曲率在交接点上发生了突变。

曲率是描述曲线上某点处弯曲程度的量。直线没有弯曲，所以直线曲率为0，圆上任意一点处的弯曲程度都相同，所以圆的曲率处处相同。

举个例子，掰筷子时总是会从中间处断开，因为中点的曲率最大，也就是弯曲程度最大。

在上述跑道圆中，半圆过渡到直线时，曲率从一个固定的正值突然变为零，这就是曲线过渡不顺滑的原因。

若要实现苹果般的顺滑效果，可使用贝塞尔曲线绘制。在软件环境中，用户可通过控制点来自由调节曲线，达到与Apple相似的效果。

日常工作中这样的跑道圆已够用，但其创建过程仅是对外部对象的描摹，缺乏逻辑上的必然性。这促使我们进一步思考：最初Apple是如何构思绘制这样一个跑道圆？这一问题引导我们探究其生成路径。

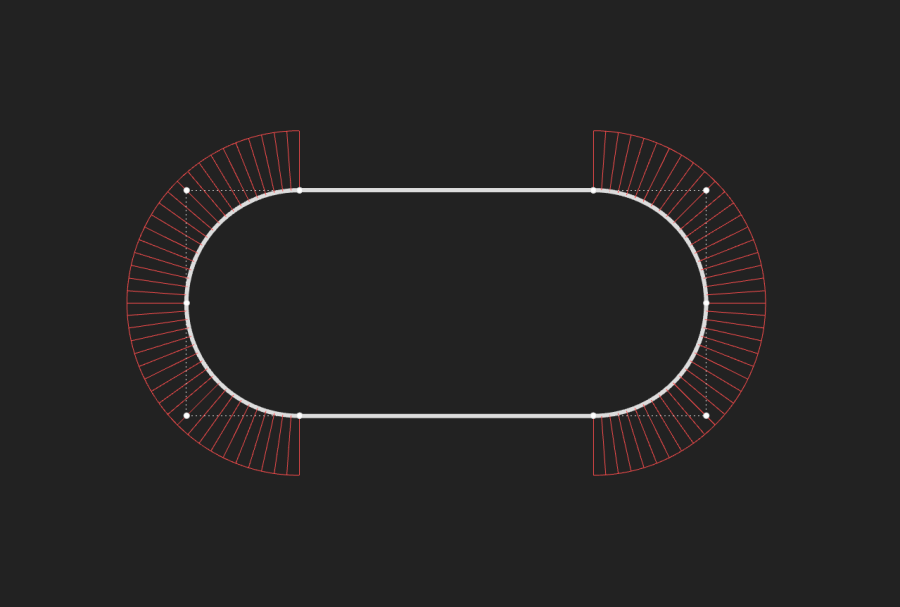
猜想：Apple使用圆弧+曲线衔接，构建跑道圆。

很容易就能想到，即然半圆与直线衔接处曲率不顺畅，那把此处截断，再使用曲线衔接，就可以构建一个我们需要的跑道圆。

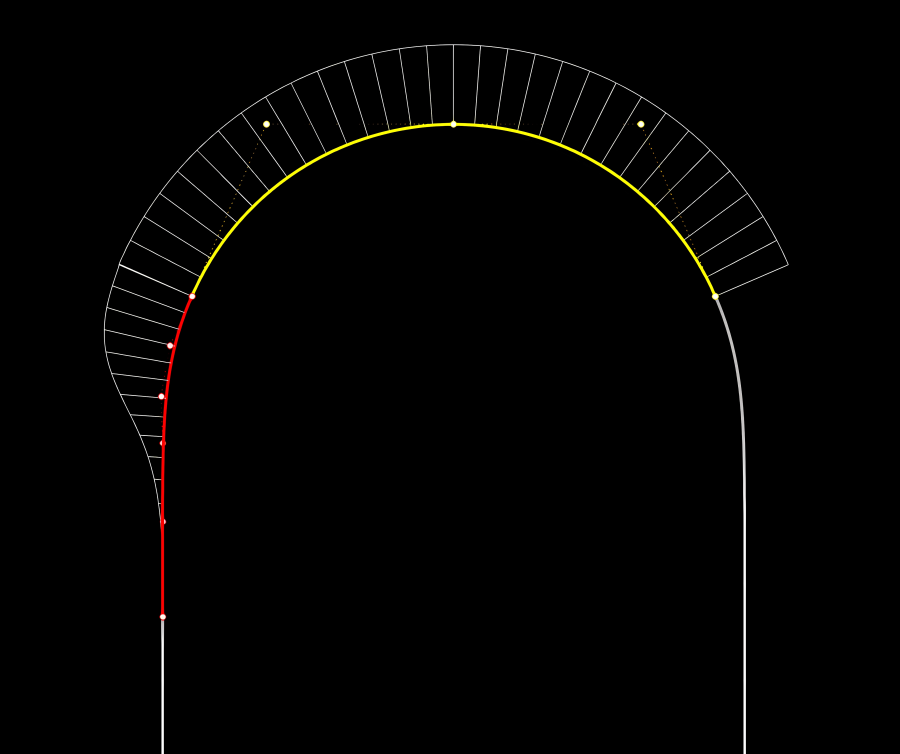
如图所示，黄色线段为正圆上截取的圆弧，红色部分的贝塞尔曲线负责与圆弧和直线衔接。这种办法简单直接好理解。

类似的方法在Apple的图形交互设计中也有应用。比如在Apple专利US9396565中展示了一种使用圆弧段与贝塞尔曲线连接，以获得图形界面中圆角矩形的动态边缘的办法。图中粉色部分为圆，绿色和黑色曲线为一条4点3阶贝塞尔曲线，R1-R4/Q1-Q4分别为曲线的4个控制点。

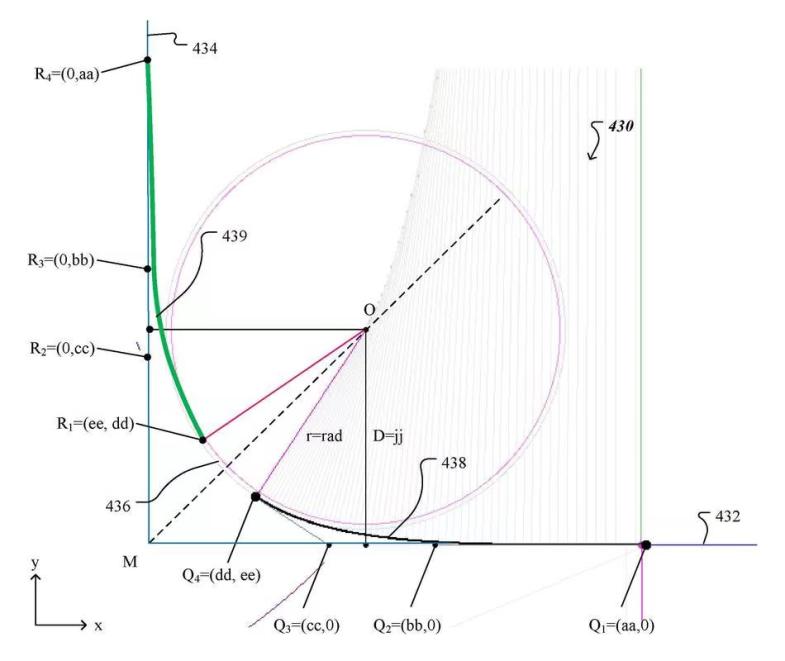
但这种办法并不是Apple硬件产品上跑道圆的生成路径。

由于图形界面的边缘是动态的，这种多段衔接的办法可提供易于变化的生成路径。但对硬件产品来说，这种办法不够简洁和本质。

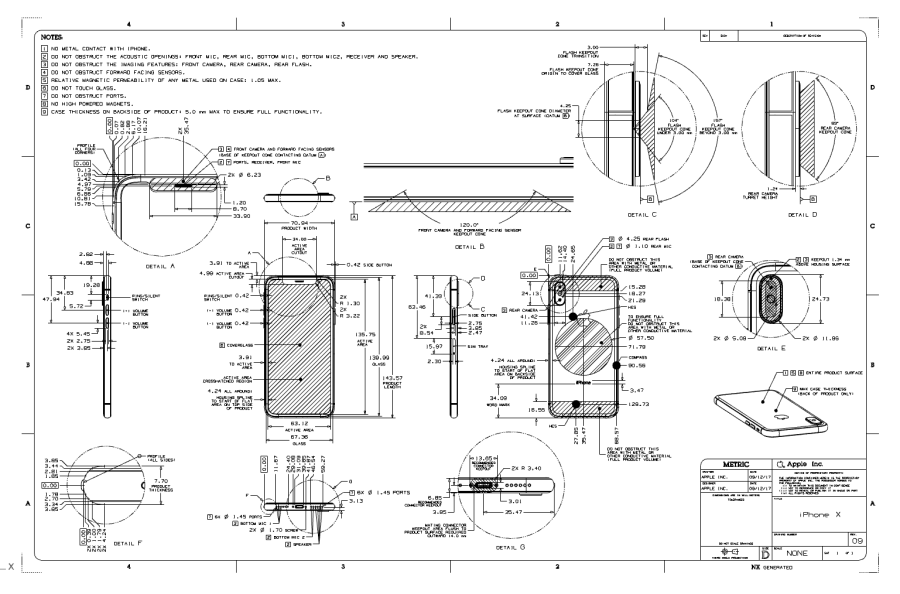
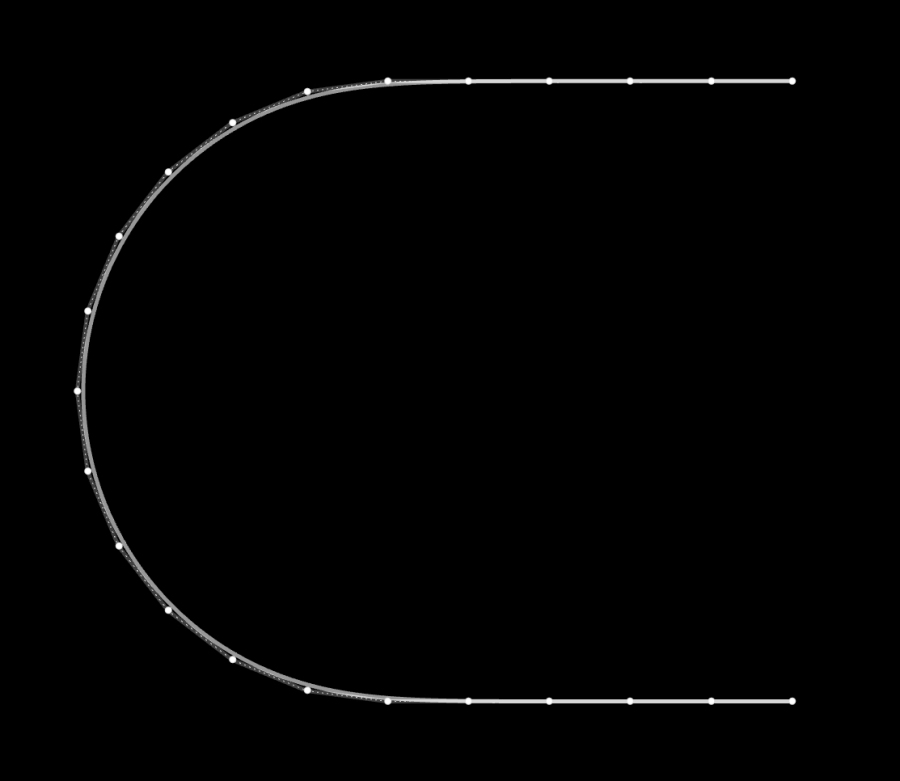
我们可在Apple公布的图纸中得到验证：硬件产品上的跑道圆，没有使用多段拼接的方法。（注：Apple提供的图纸对原始设计进行了脱敏处理，曲线被转化为很多细碎的直线段，虽无法窥探原始设计，但曲线趋势和工业模型的结构线特征得以保留，这也是研究原始设计的线索。）

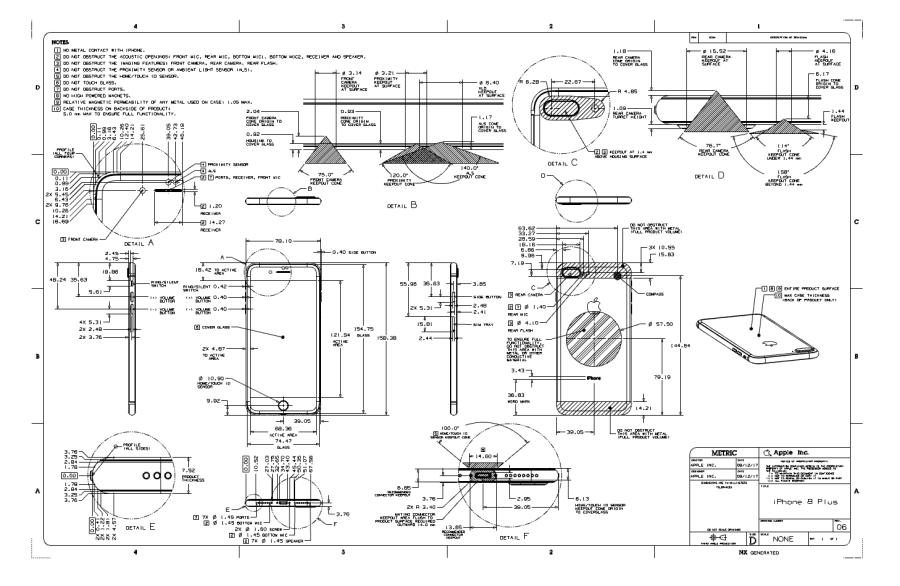
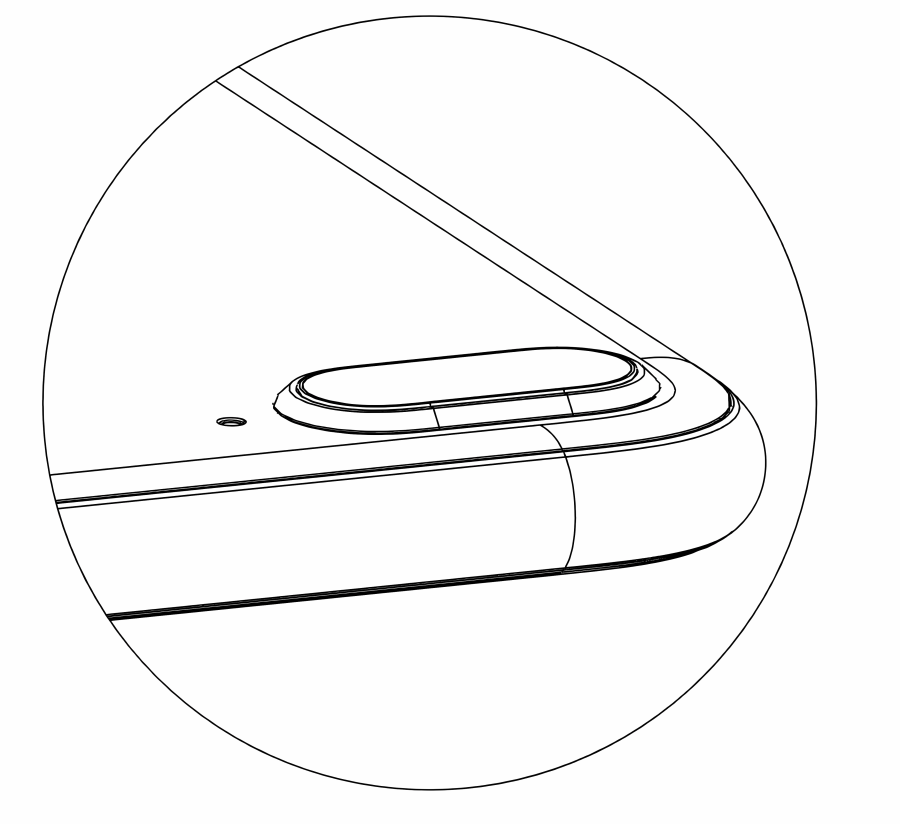
从图纸可见，Apple跑道圆由完整的类半圆曲线所构建。也就是说，我们需使用一条完整的多点贝塞尔曲线进行绘制工作。

为便于后文理解，此处需概述一下贝塞尔曲线诞生的初衷及其原理定义。

在坐标系上绘制一条曲线，如圆、椭圆、双曲线等，这些曲线都可用一组方程精确描述，这个方程就是曲线的解析方程。

也就是说，不同的形状的曲线，实质上是不同解析方程的具体表现形式，但人类任意绘制的复杂曲线不存在明确的解析方程，面对这样的曲线，最初人们想到用微分采样的方式去表达。

用许多细小直线段连接来表示曲线，只要采样频率足够高，直线段不停微分，就能无限逼近原始形状，结合点的坐标值，就能表达任意自由曲线。

但大幅提高采样频率会导致采样点数量暴增，进而引发模型数据膨胀。贝塞尔曲线的初衷，就是用尽可能少的数据来表达复杂自由曲线。

直线也是贝塞尔曲线的一种，先以最简单的直线为例，介绍一下贝塞尔曲线。

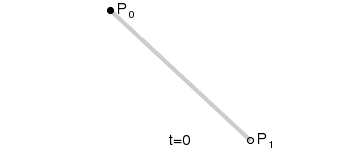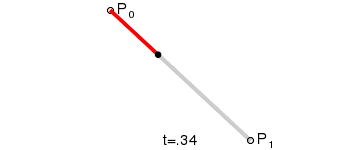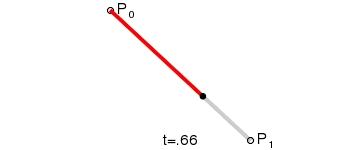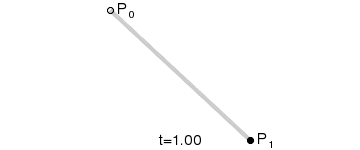
这条直线有两个端点，分别为P₀和P_1。我们都知道，两点决定一条直线，那么P₀和P₁就是这条直线的控制点。

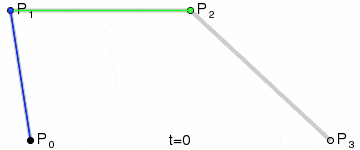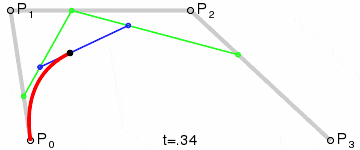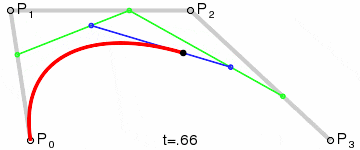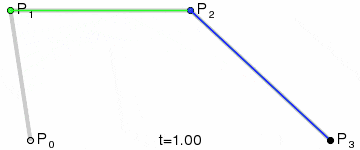
定义一个点t，经过P₀和P₁连接而成的线，连续点t所经过的轨迹，就是一条2点贝塞尔曲线。

由于这条线是通过两个控制点一次性生成的，那我们就称这条线为2点1次贝塞尔曲线，也可称为2点1阶贝塞尔曲线。

最终可得：B（t），描述一条由P₀至P₁的2点1阶贝塞尔曲线。

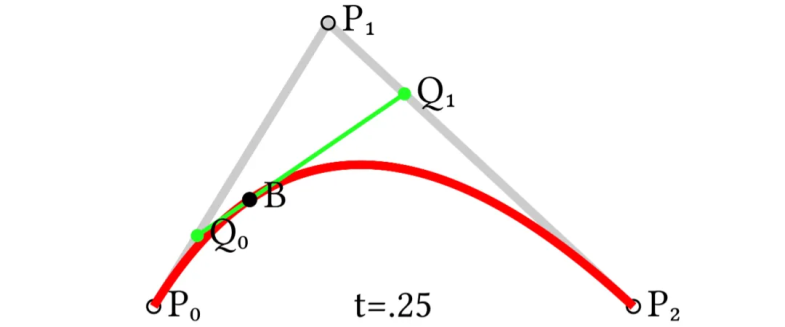
接下来我们将控制点增加到3个。

由P0至P1的连续点Q₀，描述一条1阶贝塞尔曲线。

由P1至P2的连续点Q₁，描述一条1阶贝塞尔曲线。

我们再把Q₀和Q₁连接成一条直线，定义一个点t。那么由Q₀至Q₁的连续点B（t），所经过的轨迹，就是一条3点贝塞尔曲线。

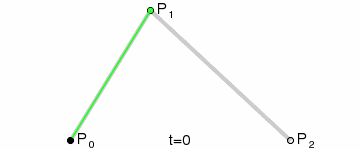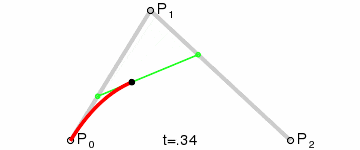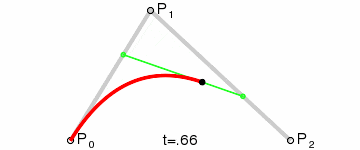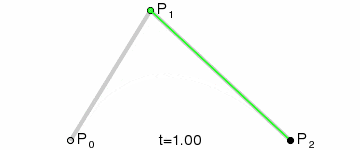
由于曲线是经过两次转换所生成，因此称其为3点2次贝塞尔曲线，也可称为3点2阶贝塞尔曲线。

以此类推，构建3阶贝塞尔曲线，就需将控制点增加到4个。

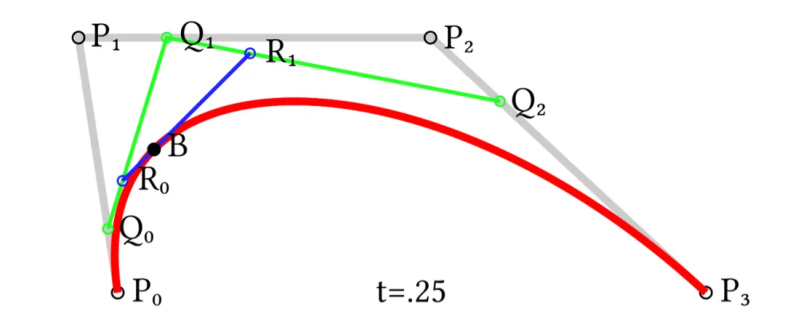
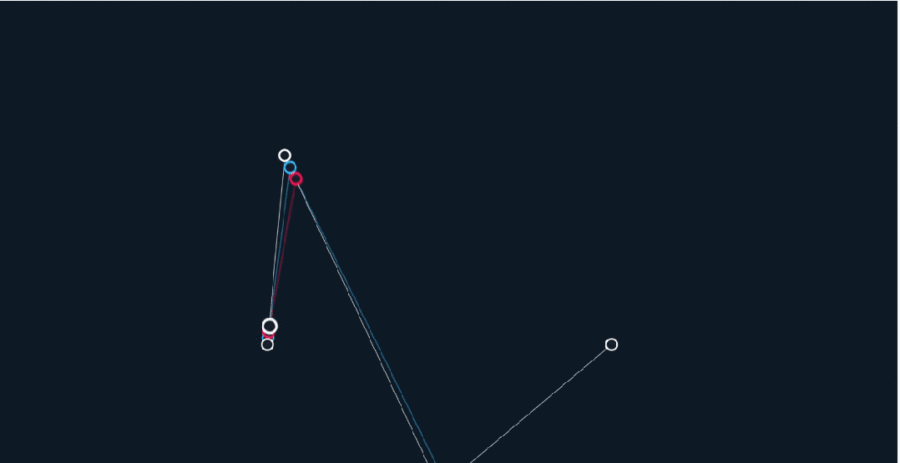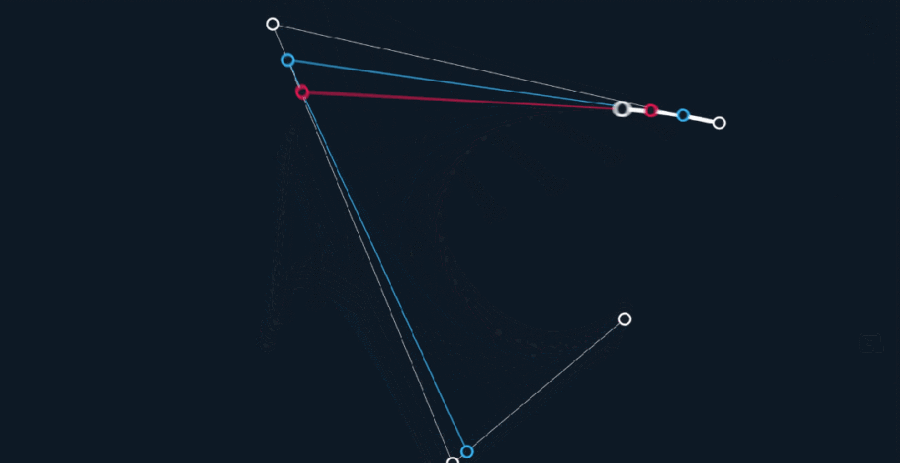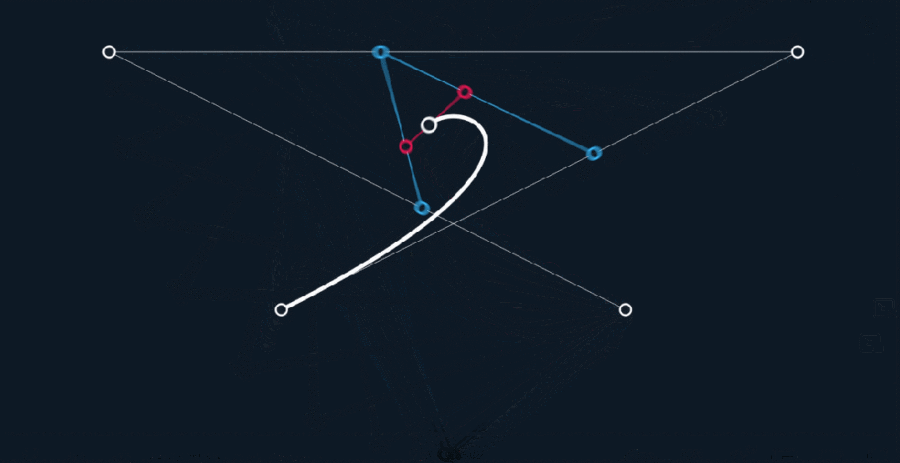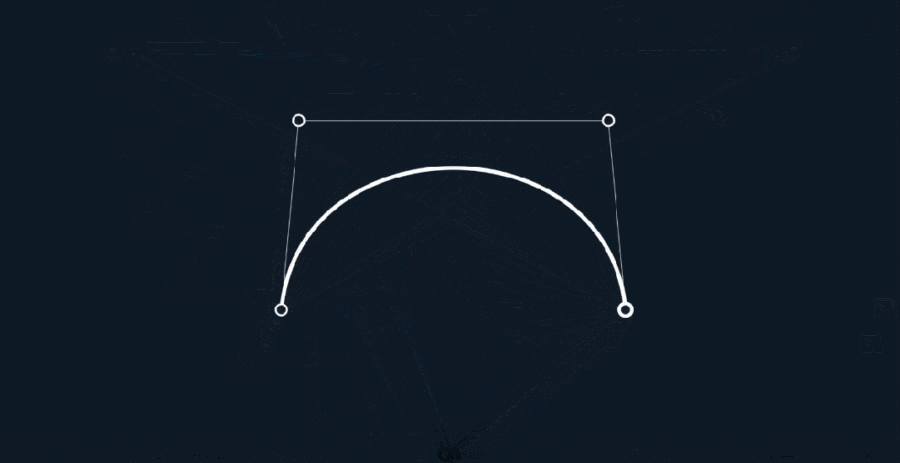
原理同上，由R₀至R₁的连续点B（t），所经过的轨迹，就是一条4点3阶贝塞尔曲线。

以此类推，更高阶的贝塞尔曲线也遵循相同的生成路径。

这样，只需得到控制点的坐标，再由相邻坐标点连接的直线段，所代表的一次线性公式，经过n次（阶）转化，就能表示一条顺滑的自由曲线，数据量大大减少。

另外，通过控制点定义曲线的方法，使得曲线调整具有很好的交互性。用户在软件中只需拖动控制点，就可自由调节曲线形状。

动画源自抖音博主：珂姬与科技

由上述内容可知：

1阶贝塞尔曲线的控制点数最少为2，

2阶贝塞尔曲线的控制点数最少为3，

3阶贝塞尔曲线的控制点数最少为4，

…

一条阶数为n的贝塞尔曲线，它的最简控制点数为n+1。

反之同样可得，n+1个控制点的贝塞尔曲线，它的最高阶数为n，最低阶数为1。

在软件中给控制点数为n+1的曲线，设定阶数小于n，看看曲线会发生什么变化。

以给定5个控制点为例，分别绘制阶数为4/3/2/1的贝塞尔曲线。如图所示，阶数越低，曲线越扭曲，越贴近控制点构成的框架。当阶数为1时，曲线成了由控制点连接成的直线段。

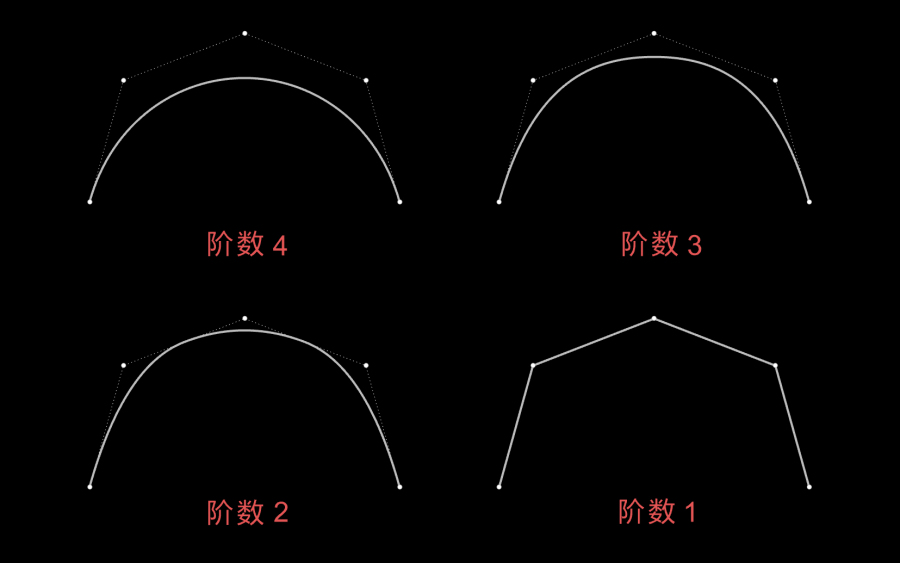
上述内容可以总结2条规律，后文调整跑道圆曲线时，会用到这两条规律。

（1）在最简控制点状态下，即阶数为n，控制点数为n+1时，曲线最为顺滑。

（2）阶数越高，由控制点连接而成的直线所代表的一次线性公式，就需要经过更多次的转化来得到曲线，这意味着阶数越高，控制点对曲线形态的影响就越“间接”。

简单点说，阶数越高，控制点对曲线形态影响的权重就越小。同理，阶数越低，控制点对曲线形态的影响越”直接“，即控制点对曲线形态影响的权重越大。

着手具体绘制工作前需先定义曲线的点数，大的原则是控制点数量越少越好，如无必要，勿增实体，每个控制点要有存在的意义。

跑道圆需满足两个条件：

（1）曲线与直线连接处需过渡顺滑。直线的曲率为0，那么曲线起始端曲率需从0开始增大。

（2）中间段要与圆相拟合，这部分需尽可能贴合圆弧。

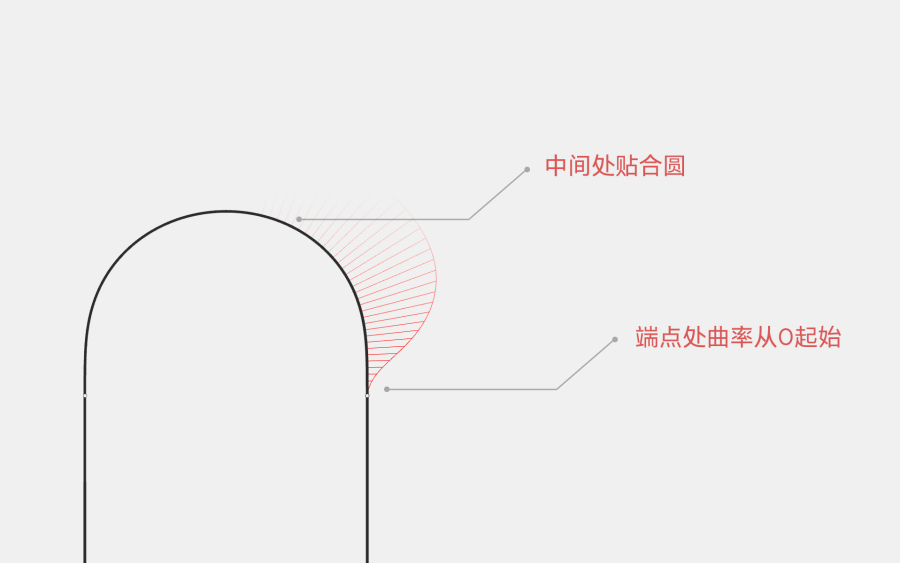
曲线起点处曲率由0开始增大，此处需满足G2连续（曲率连续）。已知与直线连接时，G2连续最少需3个控制点，且控制点共线。曲线有两端，那么此处共需3×2=6个控制点。

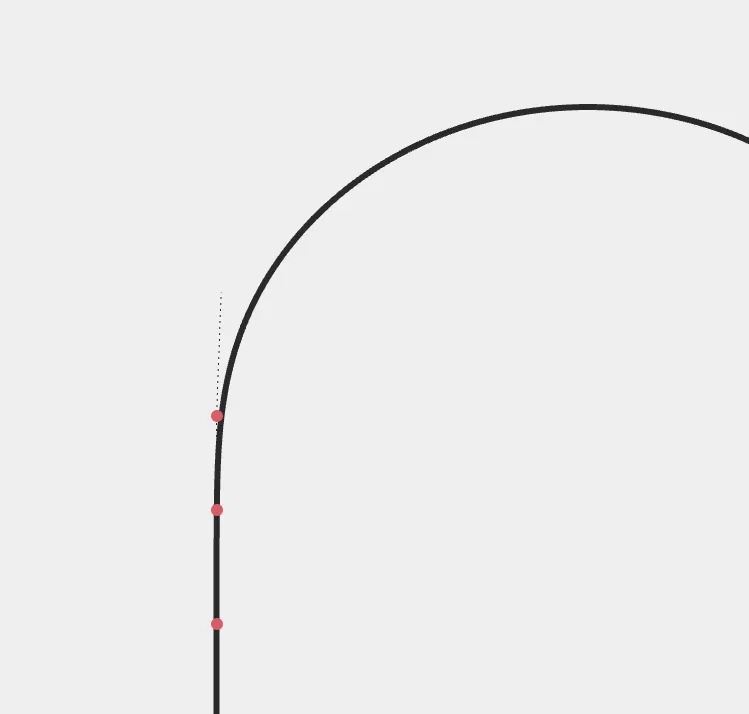
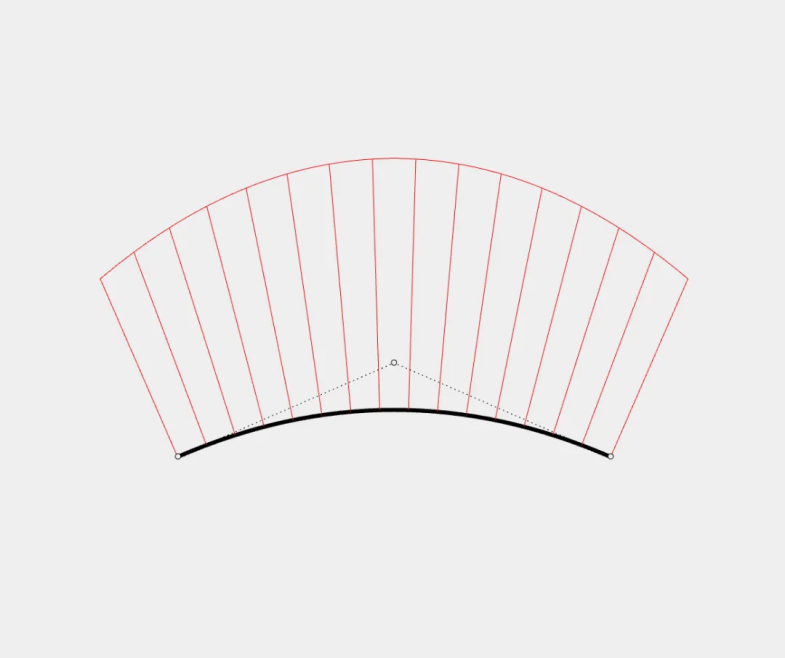
再用贝塞尔曲线拟合圆弧。本着简洁原则先用3个点来表达，但这个设定很容易推翻，一条顶点居中的3点曲线对圆弧的拟合能力非常有限，因此再增加一个点，看看4点贝塞尔曲线的表现。

在计算机图形学中，这一问题已得到深入研究并广泛应用，如Adobe  Postsc-ript环境下的平面图形和字体，都使用4点贝塞尔曲线来表达。

以Adobe illustrator为例：在Ai中绘制的“圆形”，虽然看起来像是一个平滑的几何圆，但实际上是由四段3阶4点贝塞尔曲线组成。这种用贝塞尔曲线代替真实圆的做法，是矢量图形软件中常见的技术。

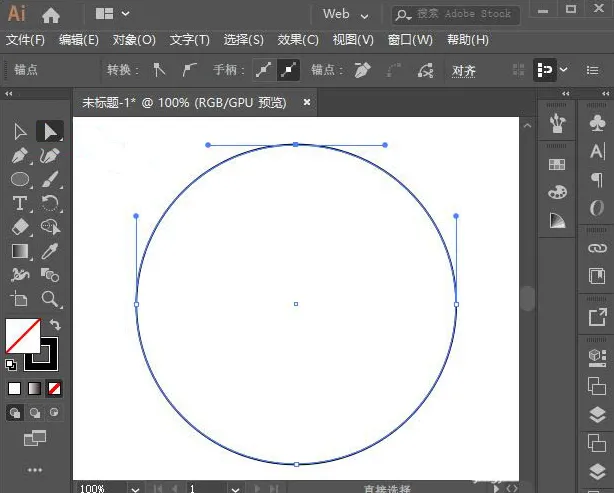
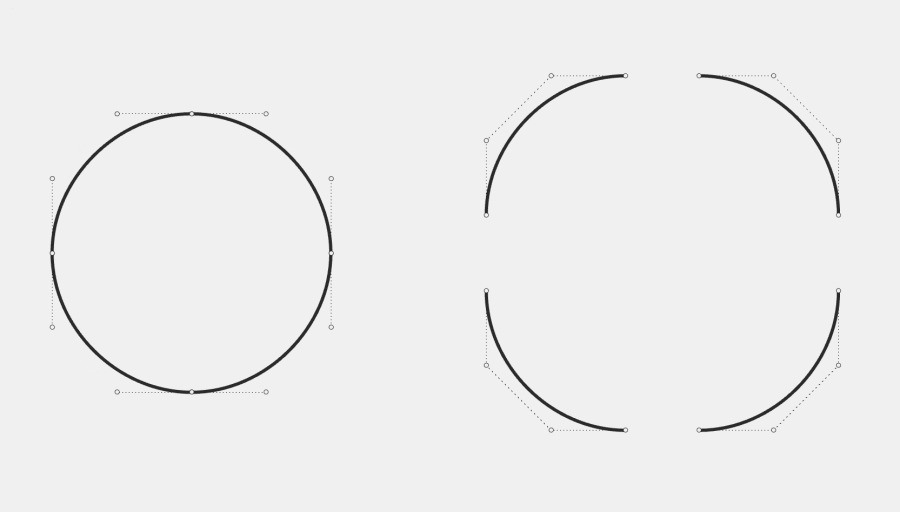
这表明3阶4点贝塞尔曲线具备优秀的拟合能力，当我们用它来拟合圆弧时，中间控制点的位置可被计算所得：曲线端点到最近控制点的最佳距离为r*4（√2-1）/3，r为圆的半径。

论证过程：

https://spencermortensen.com/articles/bezier-circle/

比如当拟合半径为1的圆时，曲线端点到最近控制点的直线距离即为4（√2-1）/3 ≈0.55228475，与标准圆弧相比，其平均落差约为1/2000，这个误差水平已经足够我们在平面印刷、产品制造等领域中应用。

误差分析过程：

https://www.cnblogs.com/ArthurQQ/articles/1730214.html

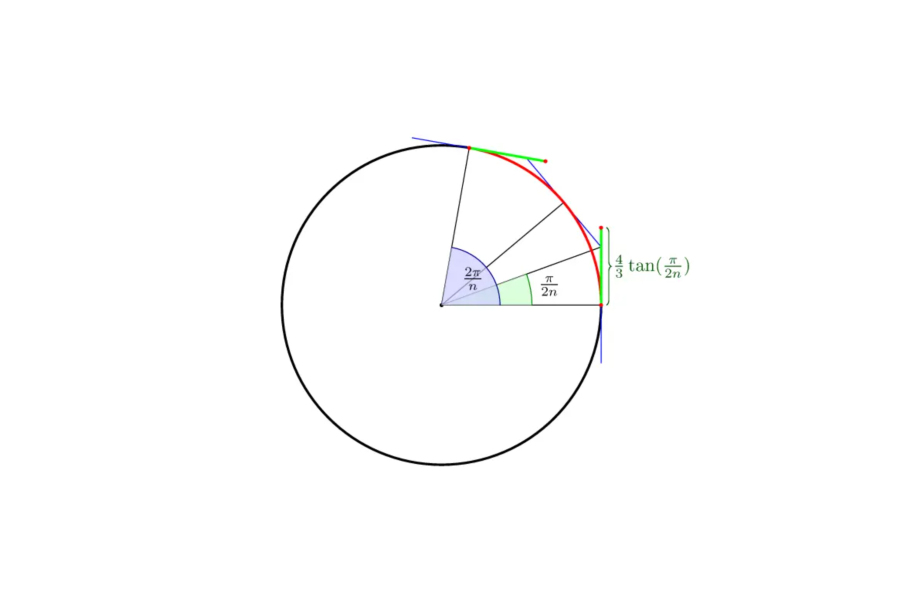
值得强调的是，用单段4点3阶曲线拟合圆弧，不同于我们本次用一条多点曲线拟合圆弧。前者4点中，有2点落在端点，而我们需要的4个点都落在中间。上述内容用来强调，4个控制点可具备很好的拟合圆弧能力，而在引入到我们本次绘制的曲线中时，由于其它6个控制点的加入，其综合调节能力会更好。

至此可知，一共所需控制点数为3×2+4=10，结合上文总结的规律1，“在最简控制点状态下，即阶数为n，控制点数为n+1时，曲线最为顺滑”，最终可知需使用9阶10点曲线。

在软件中设定曲线阶数为9、点数为10，调整后得到一个曲率过渡顺畅、中间段曲率均匀的跑道圆，看似圆满，然而，这个跑道圆还不够“圆”。

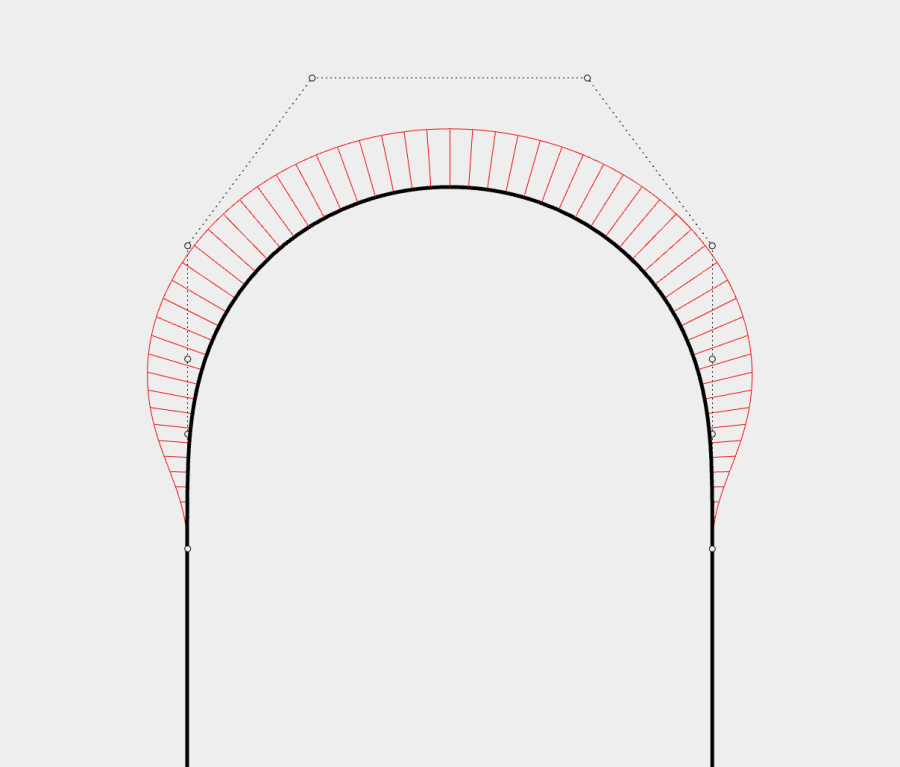
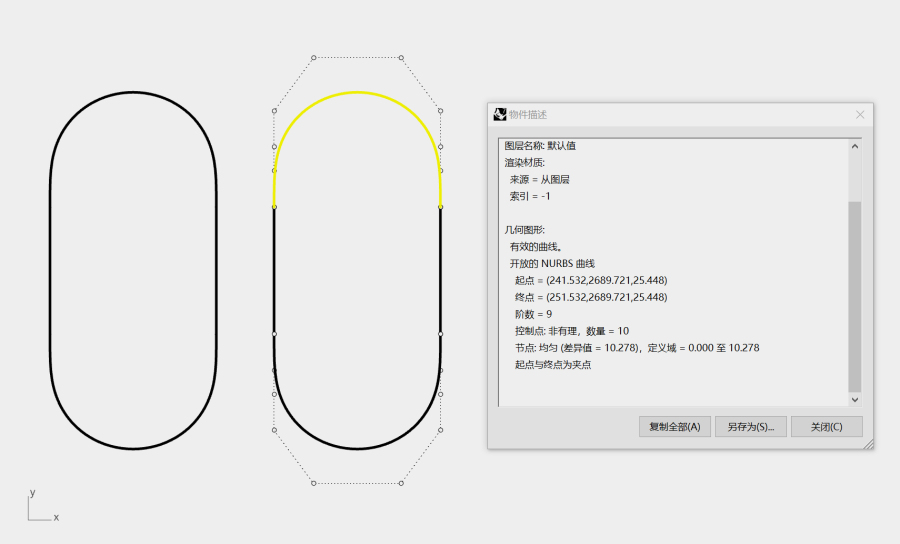
在跑道圆中放置一个逼近边缘的圆，会发现在约45度处的间距会增大。

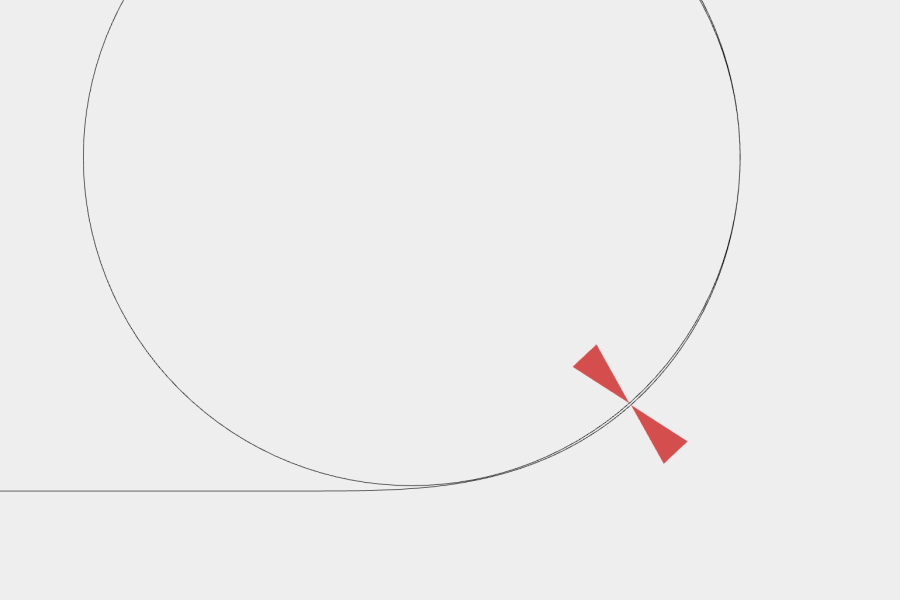
这样的跑道圆在应用时会有一点问题，例如图中的控制器设计，在约45度处的宽度略大，边缘不等距使得设计还不够尽善尽美。

而Apple的跑道圆则不存在这个问题。

多数情况下这一点点谬误无足轻重，但如果我们在乎它，就需要想办法解决它。

首先自然会想到去微调控制点，但实际操作时会发现无论如何调试，都无法将曲线与圆贴合均匀。

回顾上文总结的规律2：

“ 阶数越高，由控制点连接而成的直线所代表的一次线性公式，就需要经过更多次的转化来得到曲线，这意味着阶数越高，控制点对曲线形态的影响就越“间接”。

简单点说，阶数越高，控制点对曲线形态影响的权重就越小。同理，阶数越低，控制点对曲线形态的影响越”直接“，即控制点对曲线形态影响的权重越大。”

这就是为何我们在10点9阶状态下无法有效调控曲线。

在最简点数状态下，控制点对曲线形态影响的权重最小，即，对曲线形态的控制能力最为有限。

找出问题原因也就得到了解决路径，即然控制点权重太小，那么我们将控制点权重增大，也就是将阶数降低。

使用相同的点坐标，绘制不同阶数曲线。从阶数9到阶数1，依次排开：

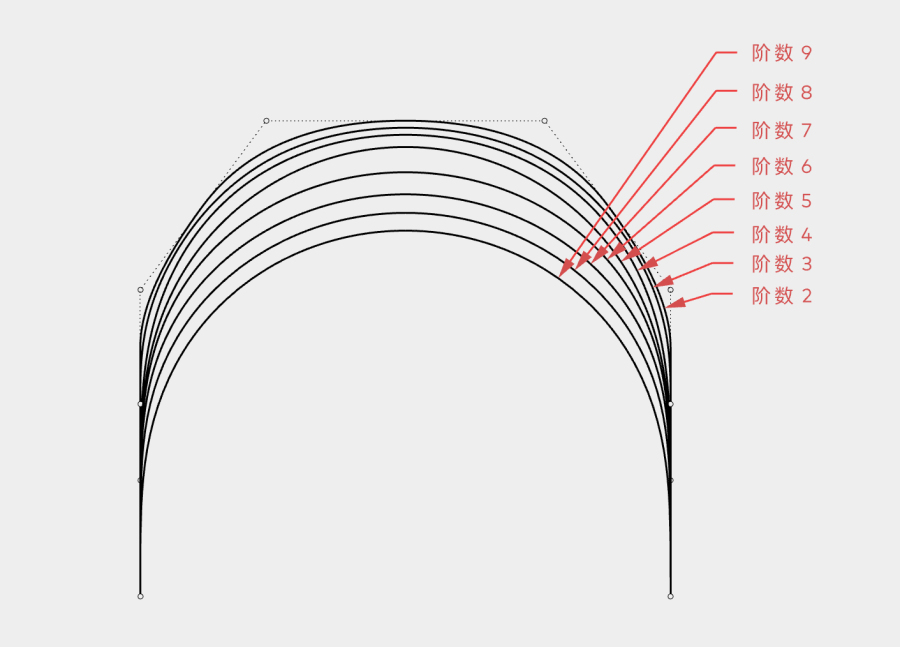
首先将阶数9、2、1给排除，剩下的打开曲率显示继续分析。

当阶数被调整时，由于控制点权重发生了变化，曲线的走势状态也随之改变。当阶数为5时，曲线拟合圆形部分的曲率高度最为均匀，也就是说，当阶数为5时，拟合圆形的效果最好。

此时我们还未调节控制点就已经达到了比较理想的状态，再稍加微调，就可以获得圆度理想的跑道圆了。

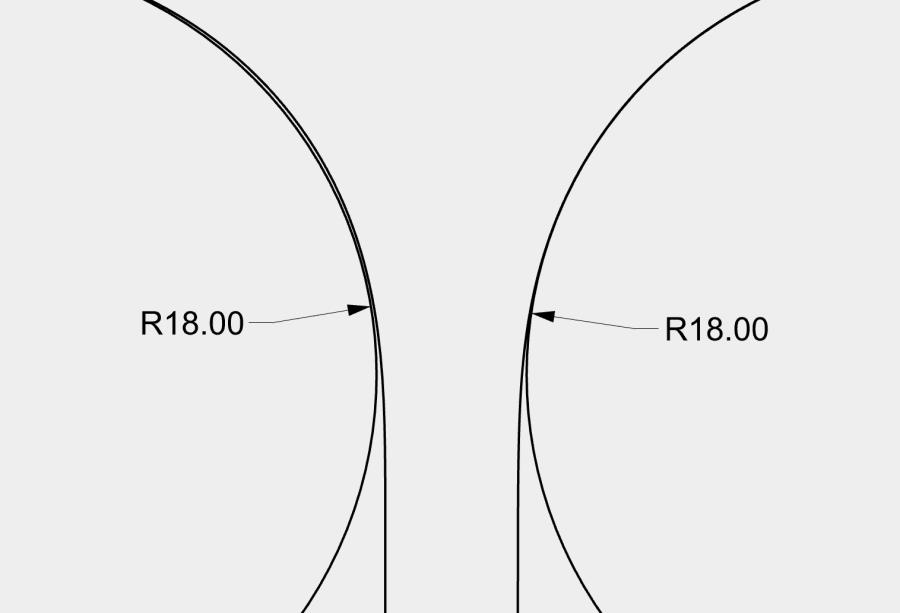
将5阶和9阶跑道圆并置展示，它们间的差异极为细微，肉眼难以察觉，但引入一个半径相同的逼近圆形比对，细微差别便跃然纸上。面对众多看似相近的选择时总会疑惑为何要特别选择其中一个，而正是这细微的“更圆”特性，显示了其存在的价值。

至此，我们将10点5阶跑道圆与iPhone 16的跑道圆进行比对，他们的轮廓完全一致。由于无法获得Apple原始设计数据，这个对比只能基于位图来完成，并不严谨，但可以确定的是，最终我们所得曲线的曲率趋势，与Apple所呈现出来的面貌，是一致的，并且它足够简洁。

但这并不是唯一的生成路径。检阅图纸可以发现一些端倪。

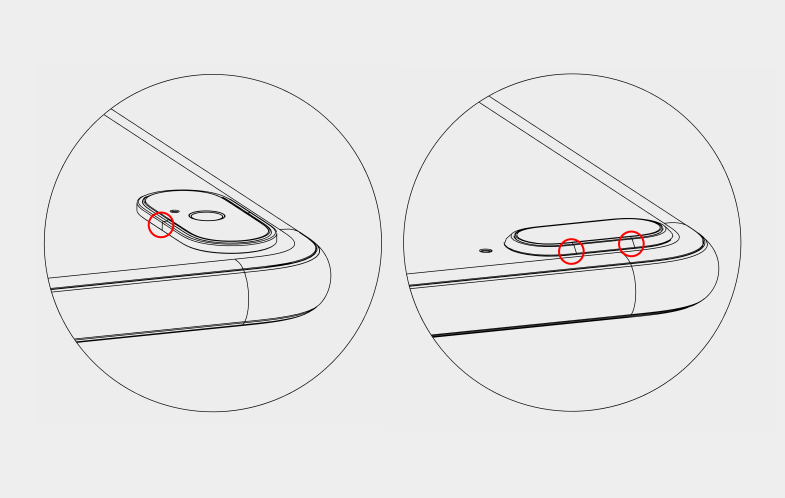
iPhone X的摄像头曲线中没有直线段，直接使用两条曲线拼接。

尽管构建方式不同，但两种跑道圆的轮廓仍然一致。这表明尽管Apple已经定义了他们所需的跑道圆轮廓，但对其具体的生成路径仍有新的想法。

这是一种以多边形的节点为控制点来绘制曲线的方法。

由本方法构建跑道圆的思路，由工业设计师陈宪原创发布，下面链接为原文地址：

https://www.puxiang.com/galleries/2e986d670ade38c1bb457493a03a5040

Apple的想法与其不谋而合，这并非偶然，因为双方都理解并巧妙运用了贝塞尔曲线。

经上文描述可发现无论低阶还是高阶，曲线总会位于控制点所形成的框架（凸包）之内，数学上称之为贝塞尔曲线的“凸包性”（convex hull property），这意味着曲线不会超出控制点构成的凸壳范围。

这个性质对计算机图形学和几何建模非常重要，因为它有助于快速判断曲线是否与某个区域相交。此外，它还保证了曲线的形状不会超出设计者预设的边界范围。

我们可以利用这个特性绘制想要的图形。比如想绘制圆角矩形的话，就可先搭建一个矩形框架，再以框架节点为控制点，便可得到圆角矩形。

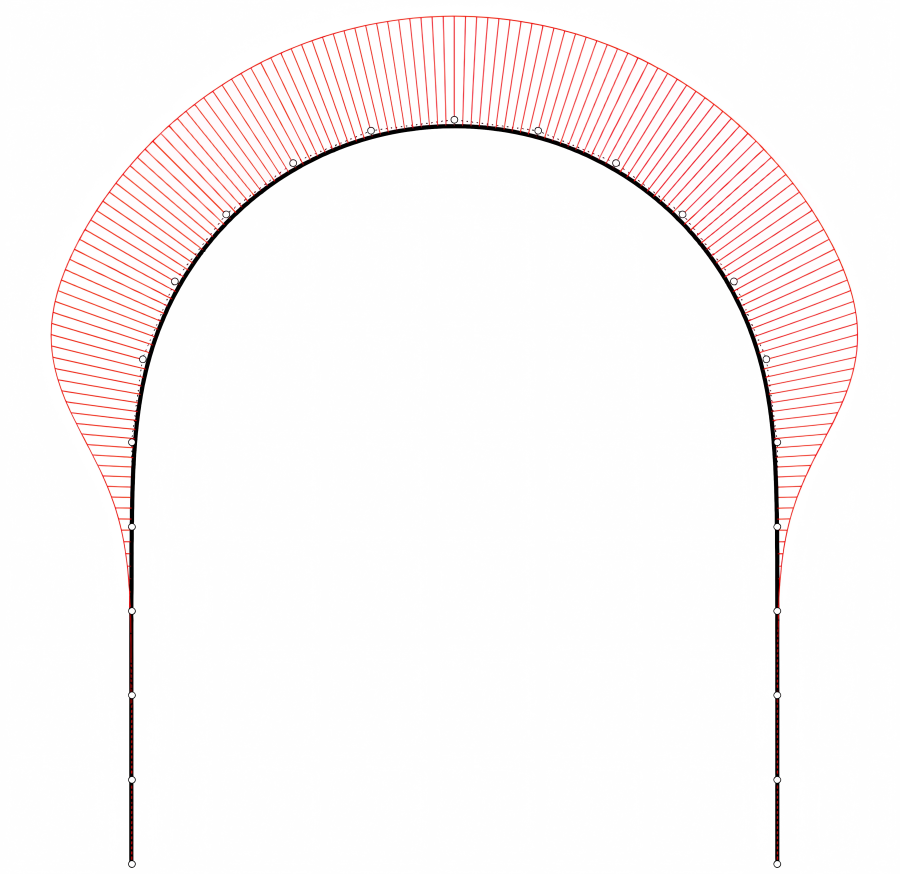
同样，想获得跑道圆，搭建跑道形的多边形框架即可。我们先构建一个正多边形，这是构建圆形的基础，再截取一半，将两端延长，延长部分同样采用等距多段的形式。

陈宪给出的方法中使用了正24边形，延长段为5个等分段，曲线设定阶数为5。多边形边数与等分段段数可自行设定，这两个元素会影响跑道圆的曲率趋势，在实际应用中可根据需求来调整。

作者在操作过程中发现陈宪原文给出的24边形5等分段状态下，圆度与曲率的视觉表现最佳，同时与apple的跑道圆也能完美契合，因此本文中也以此例为示范。

此种跑道圆的侧面通过逼近框架，达到视觉上的直边效果，但实际上不存在直线，这一特点在iPhone X的图纸中也有体现。用直线与边缘沉靠并放大观察，可见直线与边缘间有细微落差，但由于落差值远小于制造公差，因此可视作事实上有直边的跑道圆。

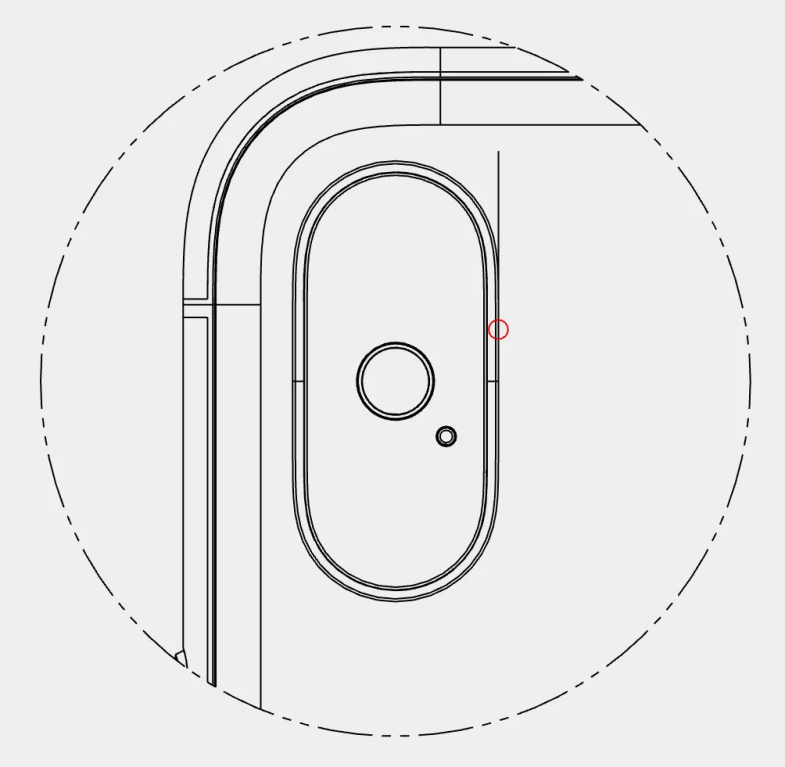
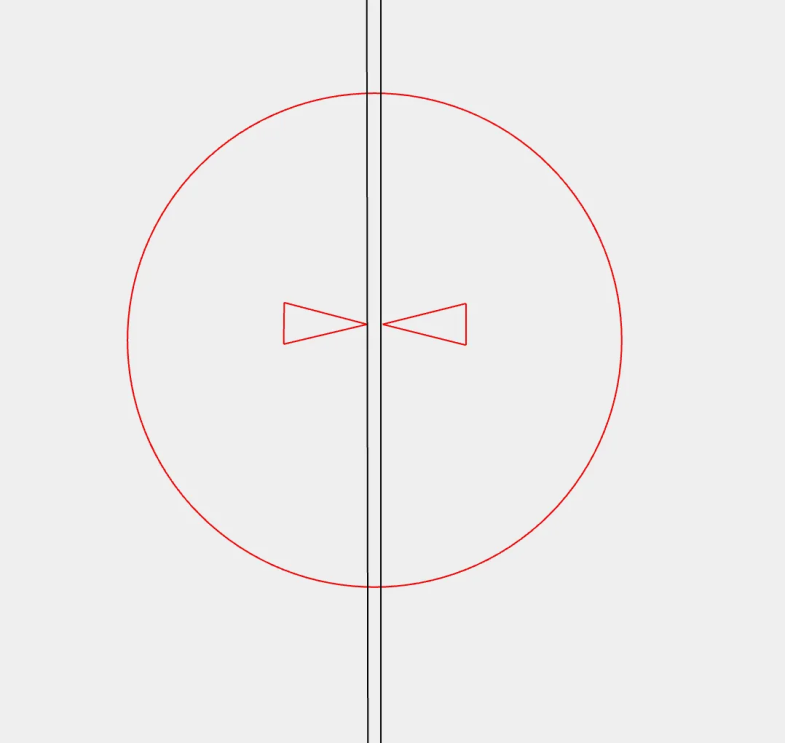
作为常见的简单几何图形，跑道圆在建筑设计、工业设计和图形交互设计中广泛应用，也正因常见，反会被人所忽视。难以想象如此纯粹的元素，为何以及如何才能打磨，而在信息充裕，设计速朽，新奇审美层出不穷的当下，刨根问底般追究这些琐碎的细枝末节，倒显得另类与无意义。

如Apple灵动岛交互上线后，一众厂商纷纷跟进，但细观其设计，却从未有品牌认真考量过其美感，所见之处尽是粗糙与随意。

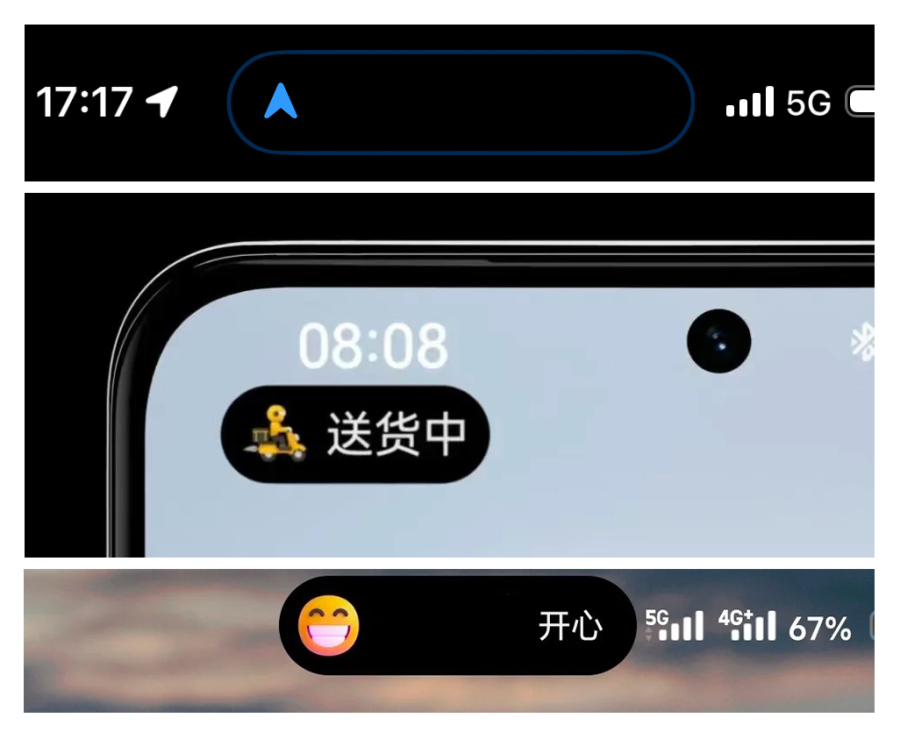
当视而不见成为习惯时，我们关注外部的，总是甚于内在的，即使讨论内在，也是为了将其转换为外部的、有利可图的营销术语。人们面对设计的态度，就是由此引申出的表现之一：在商业宣传中，设计是能被随意镶嵌在某个宏大叙事上的蕾丝花边，是廉价好用的原料佐料。可以说，是忽视和占用，共同促成了公众对设计的误解。

So what is life itself ?

百事可乐LOGO设计提案

我们并非反对设计师编织故事。设计叙事在传达产品理念与构建消费者情感联系方面具有不可或缺的价值，只是这个故事于Apple来说，就是设计成品本身，其软硬件、内外部的完整一致性，确保了设计不再是主观的装饰，而是源自核心本质的真实表达，正如柏拉图所言，“它们的美，源自其本质”。

无论是摄像头模块布局，还是灵动岛交互动画，甚至于俗常如手表的电源键，这些元素的变化之实质，在于其不变之本质，设计产出物本身，即是这静止恒定之物。

《Designed by Apple in California》序言开头：

“这本书几乎没有文字。

它讲述着我们的产品，材质的本身以及它们是如何被创造出来的。

虽然这是一本设计类书籍，但它并没有落入俗套地讲述人、故事... 而是仅仅将我们的工作坦诚地呈现出来。讽刺的是，这样的坦诚却准确地讲述了我们的工作方式、价值观、钻研精神以及我们的追求。我们所做的即是我们的一切，那么噤声是必然的。”

参考资料：

陈世栋《可以精确推演的美》

陈宪 《从多边形构建曲率圆角》

Spencer Mortensen：《Approximate a circle with cubic Bézier curves》

张吾森 译： Designed by Apple in California 引言

本文为上篇，主要讲解跑道圆的生成路径，但设计阶段的工作只是开始，下篇将介绍Apple跑道圆如何在制造中落地，那将是更为复杂的路径。